wys的个人博客

翻译

Posted on 2021-10-01 Edited on 2022-03-16 In XCPC

前言

作为本队的计算几何选手和翻译，为了找到学校训练题目中的计算几何题目，特意通过本专栏对学校训练题进行翻译。

SDKD 2021 Summer Training Series A 2nd Round

2019-2020 ICPC Northwestern European Regional Programming Contest (NWERC 2019)

A - Average Rank

在一个比赛中，每周完成的人可以得到一个点数，在每周的末尾，会对每个人的到的点数进行排名。每个人的排名为分数大于他的人数$+1$ , 如果两个人得到的点数相同那么他们的名次相同。

一共有n名参赛选手，比赛进行w周，每周给你一个选手的得分列表，你的任务是计算n名选手在这w周的平均名次。

输入

第一行n,w，分别表示人数和周数。

接下来w行，第 $i$ 行开头为 $k$，接下来k个数字$c_1,…c_k$表示$c_1,…,c_k$名选手在第 $i$ 周得到一分。

所有选手的总共得分不超过 $1 million$。

输出

$n$行，第$i$行表示第$i$名选手的平均名次。

B - Balanced Cut

给你一棵 $n$ 个结点的平衡二叉搜索树，该树具有如下性质：

左右子树深度之差不超过1。
结点的值比左子树中所有结点的值都大，比右子树所有结点的值都小。

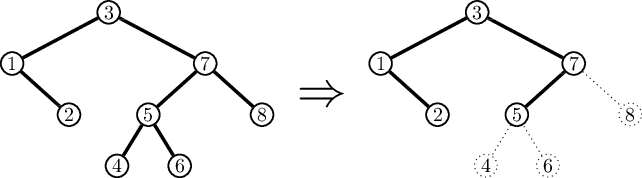
现在让你删除结点至只剩 $k$ 个结点，当你删除结点时，所有该节点的子孙结点将被删除。

先让你完成这个操作，使剩余结点的中序遍历字典序最小。

输入

$n,k$ 表示有$n$个结点，要求剩余$k$个结点。

接下来 $n$ 行，第$i$行为 $p_i$ ,表示值为 $i$ 的结点的父亲的值为$p_i$, $p_i$ 为 $-1$ 表示为根节点。

输出

一个字符串，第 $i$ 位为$0$表示删除，为 $1$ 表示保留。

D - Disposable Switches

给一个 $n$ 个结点，$m$ 条路径的无向图，表示一个网络。每根传输时间为 $l/v + c$ , $l$ 为电缆的长度，$v$ 为传输速率，$c$ 为常量，$v$ 和 $c$ 未知，只知道$v > 0$ , $c >= 0$ ，当一个数据传送到一个结点时，他会选择路径耗时最短的结点进行转发，求无论 $v$,$c$ 为何值时，从$1$发送数据到$n$，有哪些结点是永远不会被转发到的。

输入

$n$,$m$ ,表示有 $n$ 个结点，$m$ 条路径。接下来 $m$ 行，每行有三个数 $a$ , $b$ , $l$ ,表示 $a$ 到 $b$ 之间的电缆长度为 $l$。

无重边，自环。图保证联通。

输出

第一行为一个 $k$ ,第二行有$k$个数，表示有$k$ 个结点不会被转发到。输出按升序排列。

SDKD 2021 Autumn Training Series B 1st Round

2018 German Collegiate Programming Contest (GCPC 18)

A - Attack on Alpha-Zet

给你一个二维网格平面，每格是一个 $1 \times 1$ 的单元格，每个单元格至少有一个和他相邻的单元格，单元格两两之间存在路径，并且不存在环。在这个二维平面中依次访问 $n$ 个点，求最少走过的单元格。

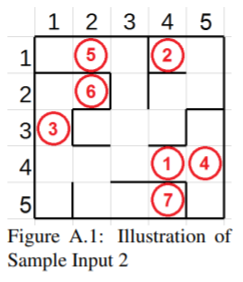
输入

第一行为 $h,w (2\leq h,w\leq 1000)$ 。表示迷宫的高和宽。

接下来 $h+1$ 行用$ASCII$表示一个迷宫，每行有$2 \cdot w+1$ 个字符。规则如下：

奇数行表示一个竖墙或者空格。偶数行表示一个横墙或者空格。
第一行为最北边的墙，只由横线构成，接下来的行都表示单元格。
单元格都在偶数列，左右为竖墙，如果没有竖墙则用空格代替。

接下来一行是一个数字 $m$ 。

接下来 $m$ 行，第 $i$ 行表示第 $i$ 要到达的点。每个坐标可能出现多次。$(1,1)$ 为左上角的点 $(h,w)$ 为右下角的点。

保证迷宫是封闭的，且两个点之间只有一条路径。

输出

一个数字，表示要走过的单元格。

B - Battle Royale

给你个蓝色圆，和一个红色圆。问从$A$ 走到 $B$ 最短路径。

输入

$a$ 点坐标，$b$ 点坐标，蓝圆圆心坐标和半径，红圆坐标与半径。

$a$, $b$ 点保证在蓝圆内，红圆外。

输出

最短路径，误差不超过 $10^{-7}$ 。

C - Coolest Ski Route

给一个有向图，让你求一条权值最大的路径。

输入

$n,m$ 表示有 $n$ $(2 \leq n \leq 1000) $个点， $m$ $(1 \leq m \leq 5000)$条边。

接下来 $m$ 行，每行分别为 $s,t,c(1\leq s,t \leq n,1 \leq c \leq 100)$ ,分别表示起点终点和权值。

输入保证没有回路。

输出

一个整数，表示最长路径。

D - Down the Pyramid

一个金子塔形状的图案，相邻的两个单元格相加为上层单元格数值，现告诉你 $n$ 层的序列，让你求 $n+1$ 层有几种可能。

输入

$n(1 \leq n \leq 10^6)$

$n$ 个数表示这个序列。

输出

一个数字，表示下一行有几种可能。

E - Expired License

给你 $a,b$ 问你能否找到两个素数$p,q$，使得 $\frac{p}{q} = \frac{a}{b}$。

输入

$n(1 \leq n \leq10^5)$

接下来 $n$ 行，每行有一个$a,b(0 < a,b < 100)$ 。小数点后最多五位小数。

输出

满足条件的 $p,q$，如果不存在输出$impossible$ ，如果有多组解，输出 $p+q$ 最小的情况。

F - Fighting Monsters

两个怪物互相攻击，，每个怪物有一个血量，当怪物 $A$ 攻击怪物 $B$ 时，会对$B$造成$A$血量的伤害。

攻击过程如下图所示：

现在给你 $n$ 个怪物，问你能不能找到两个怪物，互相攻击使其中一个血量只剩下$1$点。

输入

$n(2 \leq n \leq 10^5)$

第二行为$n$个数，表示$n$个怪物的血量。

输出

两个怪物的下表$i,j$，如果不存在输出$impossible$。如果存在多个，输出任意。

In-Circle

Posted on 2021-09-28 Edited on 2022-03-16 In 计算几何大师之路

uva 11524

题意

如图所示， $\triangle{ABC}$ 的内切圆把他的三边分别划分成 $m1:n1$ , $m2:n2$ ,$m3:n3$ 的比例。另外已知内切圆的半径 $r$ ,求 $\triangle{ABC}$ 的面积。

普遍思路

设三角形三边长为 $a$ , $b$ , $c$ 。

由内切圆得三角形的面积为 $S = \frac{(a+b+c)*r}{2}$ 。

由海伦公式得三角形得面积为 $S = \sqrt{p(p-a)(p-b)*(p-c)}$ 。

其中 $p = \frac{a+b+c}{2}$ 。

设 $AP$ 为$m_1x$联立两个方程可以解出 $x$ 从而可以求出答案。

个人思路

个人认为上述方程比较难解，下面给出另一种解法。

在三角形中有如下结论

$\tan{\frac{A}{2}}\tan{\frac{B}{2}}+\tan{\frac{A}{2}}\tan{\frac{C}{2}}+\tan{\frac{B}{2}}*\tan{\frac{C}{2}} = 1$

$\therefore \frac{1}{\tan{\frac{A}{2}}} + \frac{1}{\tan{\frac{B}{2}}} + \frac{1}{\tan{\frac{C}{2}}} = \frac{1}{\tan{\frac{A}{2}}\tan{\frac{B}{2}}\tan{\frac{C}{2}}}$

而 $\tan{\frac{A}{2}} = \frac{r}{y}$ , $\tan{\frac{B}{2}} = \frac{r}{z}$, $\tan{\frac{C}{2}} = \frac{r}{x}$

代入上式得 $\frac{x+y+z}{r} = \frac{xyz}{r^3}$

即可解出答案。

代码

#include <bits/stdc++.h>
#define FOR(i,f_start,f_end) for(int i=f_start;i<=f_end;++i)
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int>PII;
const double eps = 1e-8;
const int maxn = 200000 + 5;
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
//unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
//mt19937 rand_num(seed);



int main(){
    
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);

    //std::ios::sync_with_stdio(false);
    int t;
    cin >> t;
    while(t--){
        double r;
        cin >> r;
        double m1,n1,m2,n2,m3,n3;
        cin >> m1 >> n1 >> m2 >> n2 >> m3 >> n3;
        double p,q;
        p = m2*m2*m1*n2/n1/r/r;
        q = (n1*m2+m1*m2+n1*n2)/n1;
        double x = sqrt(q/p);
        double l = (2*m2 + 2*n2 + m1*m2/n1 + n2*n3/m3)*x/2;
        printf("%.4lf\n",l*r);
    }
    return 0;
}

atan与atan2

Posted on 2021-09-27 Edited on 2022-03-16 In 计算几何大师之路

atan2

atan2 是一个四象限函数。

atan2 的给定参数为 $y$ , $x$ ,需要注意的是 atan2 的参数前面为 $y$ , 后面为 $x$ 。

当 $x$ , $y$ 分别在四个象限时，返回值如下图所示。

其大小按箭头方向递增

atan

atan 是一个双象限函数。

atan 的给定参数为 $y/x$ 。

主要要对 x == 0 时进行特殊讨论 。当 $x$ , $y$ 分别在四个象限时，返回值如下图所示。

我们可以用如下程序对 atan 进行转化，将其转化为一个四象限函数。

double cal(int x,int y){
	if(x==0)return y>0?pi/2:-pi/2;
	if(y==0)return x>0?0:pi;
	double ans=atan(double(y)/x);
	if(x>0)return ans;
	return ans+pi;
}

转化后大小按如下箭头方向递增。

P1142 轰炸

Posted on 2021-09-19 In 计算几何大师之路

思路一

考虑到数据范围比较小，我们考虑尝试 $\mathcal{O}(n^3)$ 的做法，枚举两个点确定一条线段，然后枚举第三个点，用外积判断三角形的面积是否 $0$，如果外积为 $0$ ,则说明该点在直线上，在洛谷上提交时，如果 $k$ 不从 $j+1$ 开始循环会 $tle$ 三个点，如果不开 $o2$ 优化会 $tle$ 一个点。

代码

#include <bits/stdc++.h>
#define FOR(i,f_start,f_end) for(int i=f_start;i<=f_end;++i)
#define pb push_back
using namespace std;

计算几何模板(持续更新)

Posted on 2021-09-18 Edited on 2021-10-01 In 计算几何大师之路

1.计算叉积

double corss(PDD a,PDD b){
    return a.x*b.y - a.y*b.x;
}

当 $a$ 在 $b$ 的逆时针方向时，叉积为正，当 $a$ 在 $b$ 的顺时针方向时叉积为负

2.计算三角形面积

1
2
3

double area(PDD a,PDD b,PDD c){
    return corss(b-a,c-a)/2;
}

这里计算的时三角形的有向面积，当 $ab$ 在 $ac$ 逆时针方向时面积为正，顺时针方向时面积为负。

I- Error Correction

Posted on 2021-09-13 Edited on 2021-09-27 In XCPC题解

2019-2020 ACM-ICPC Pacific Northwest Regional Contest (Div. 1)

题目是给定一个字符串集合，求一个最大的集合，该集合中的元素满足不能交换任意两个字符，使之成为集合中的另一个元素。

我们考虑将能交换两个字符使其中一个字符串$s1$变为另一个字符串$s2$,的两个字符串连边。那么题中的条件可以转化为求一个最大的点集，使这个点集中的元素两两没有连边。即求该图的最大独立集。判断两个字符串是否可以连边，我们可以判断两个字符串是否只有两个字符不同。因为所有字符串之间为$anagram$^footnote。

我们考虑朴素的最大独立集算法，时间复杂度为$\mathcal{O}(3^{n/3})$，提交后收获一发$TLE$。

B. lucky probability

Posted on 2021-09-11 Edited on 2021-09-27 In Codeforces题解

Codeforces Beta Round #84 (Div. 1 Only)

思路

我们先考虑生成所有九位以内的仅有4和7组成的数。

对于我们考虑枚举起点，取其中连续的k个数。

我们假设起始数为 a[i]。则终止数为 a[i+k-1]。

我们设 f(x,y,u) 为 [x,y] 中大于等于u的数的个数。

g(x,y,u) 为[x,y] 中小于等于u的数的个数。

则总的数量为

$(f(p_l,p_r,a[i])-f(p_l,p_r,a[i-1]))*(g(v_l,v_r,a[i+k-1])-g(v_l,v_r,a[i+k]))$ $+$ $(f(v_l,v_r,a[i])-f(v_l,v_r,a[i-1]))*(g(p_l,p_r,a[i+k-1])-g(p_l,p_r,a[i+k]))$

最后我们需要特判一种情况

即当k为1时，如果设这个数为x，如果x∈[p_l,p_r],并且x∈[v_l,v_r]，那么总的数量需要减一。因为第一个区间取x，第二个区间取x 和第二个区间取x，第一个区间取x重复。