迭代器和连接

1 导言

让我们从最简单的问题开始：连接到底是什么？如果您还记得SQL项目，您将记得在R.name=S.name上编写R内部连接S和其他类似的语句。

实际上，这意味着，你需要两个关系，R和S，并从它们在连接条件上的匹配中创建一个新关系——也就是说，对于R中的每个记录$r_i$，找到S中与我们指定的连接条件匹配的所有记录$s_j$，并将＜$r_i$，$s_j$＞写入输出中的新行（R的所有字段后面跟着S的所有字段）。SQL讲座幻灯片是一个很好的资源，可以让您更清楚地了解连接实际上是什么。

在讨论不同的连接算法之前，我们需要讨论当由＜$r_i$，$s_j$＞组成的新连接关系形成时会发生什么。无论何时计算联接的成本，我们都会忽略将联接关系写入磁盘的成本。这是因为我们假设连接的输出将被稍后执行SQL查询时涉及的另一个操作符使用。通常，此运算符可以直接从内存中使用连接的记录。如果这听起来让人困惑，不要担心；我们将在查询优化模块中重新讨论它，但现在需要记住的重要一点是，最终写入成本不包括在联接成本模型中

求和并没有告诉我们任何我们不知道的事情；我们需要通过每一轮，准确地找出读写的内容。最后的2X部分表示，为了构建哈希表，我们需要在分区通过后读取和写入每个页面。

以下是一些重要属性：

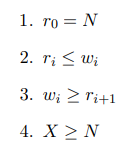
属性1表示我们必须在第一次分区过程中读取每个页面。这直接来自算法。

属性2表示，在分区过程中，我们将写出至少与读入一样多的页面。这直接来自上面的解释——我们可以在分区过程中创建额外的页面。

属性3表示我们不会读取比之前分区过程中写入的页面更多的页面。在最坏的情况下，pass i中的每个分区都需要重新分区，因此这需要我们读取每个页面。然而，在大多数情况下，一些分区将足够小，以容纳内存，因此我们可以读取比上一次生成的页面更少的页面。

属性4表示我们将构建哈希表的页面数量至少与我们开始时的数据页面数量一样多。这是因为分区过程只能增加数据页的数量，而不能减少它们。

2 简单嵌套循环连接 SNLJ

让我们从最简单的策略开始。假设我们有一个B页缓冲区，我们希望在连接条件θ下连接两个表R和s。从最自然的策略开始，我们可以在R中获取每个记录，在S中搜索其所有匹配项，然后生成每个匹配项。

这称为简单嵌套循环连接（SNLJ）。您可以将其视为两个嵌套的for循环：

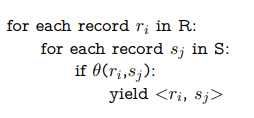
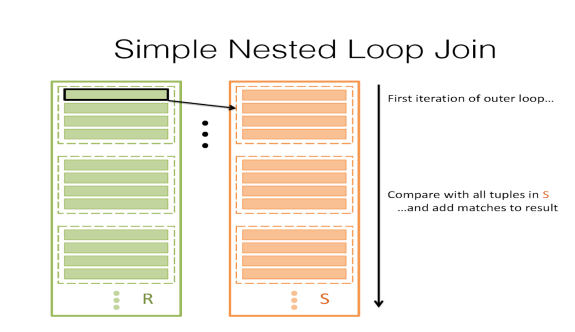
这将是一件很好的事情，但该类的主题实际上是围绕优化和最小化I/O。因此，这是一个非常糟糕的方案，因为我们在R中获取每个记录，并在S中读取每个页面以搜索匹配项。这样做的I/O成本将是[R]+|R|[S]，其中[R]是R中的页数，|R|是R中记录的数量。虽然我们可以通过在for循环中切换R和S的顺序来稍微优化，但这确实不是一个很好的策略。

注意：SNLJ不会产生|R| I/o来读取R中的每一条记录。这将花费[R]I/o，因为它实际上更像是“R中的每个页面$p_r$:$p_r$中的每个记录r:S中的每个页$p_s$:$p_s$中每个记录s:join”，因为我们不能一次读取少于一页。

3 页嵌套循环连接 PNLJ

很明显，我们不想为R的每一条记录读取S的每一页，那么我们能做得更好吗？如果我们读S中的每一页，而读R中的每页，会怎么样？也就是说，对于R的一页，获取所有记录并将它们与S中的每个记录进行匹配，然后对R的每一页执行此操作。

这称为页面嵌套循环连接（PNLJ）。下面是它的伪代码：

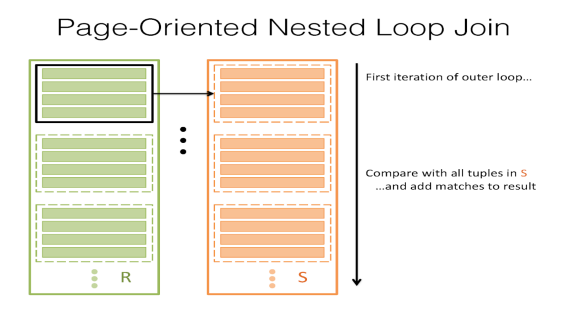
这样的I/O成本稍微好一些。它是[R]+[R][S]——这可以通过保持R和S之间的较小关系作为外部关系来优化。

4 块嵌套循环连接 BNLJ

页面嵌套循环连接更好！唯一的问题是我们仍然没有尽可能充分地利用缓冲区。我们有B个缓冲页，但我们的算法只使用了3个缓冲页——一个用于R，一个用于S，另一个用于输出缓冲区。请记住，我们在S中读取的次数越少越好——因此，如果我们可以为R保留B-2页，并将S与每个“块”中的每个记录进行匹配，我们可以大幅降低I/O成本！

这称为块嵌套循环联接（或块嵌套循环连接）。这里的关键思想是，我们希望利用缓冲区来帮助我们降低I/O成本，因此我们可以为R块保留尽可能多的页面——因为我们每个块只读取S的每个页面一次，更大的块意味着更少的I/O。对于R的每个块，将S中的所有记录与块中的所有纪录进行匹配。

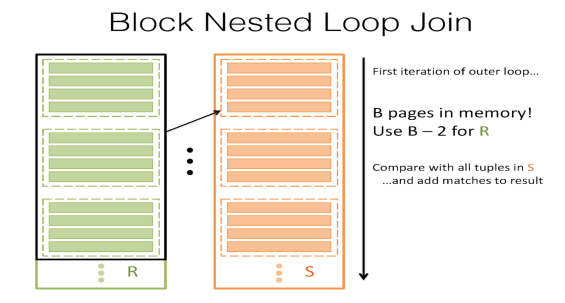
然后，其I/O成本可以写为

$[R] + \lceil \frac{[R]}{B-2} \rceil[S]$

这好多了！现在，我们利用我们的B缓冲页来减少我们必须在S中读取的次数。

5 索引嵌套循环连接 INLJ

然而，有时块嵌套循环连接不是最好的选择。有时，如果我们在S上有一个索引，该索引位于适当的字段（即我们要加入的字段）上，则在S中查找$r_i$的匹配可能非常快。这称为索引嵌套循环连接，伪代码如下：

I/O成本为[R]+|R|∗（以S为单位查找匹配记录的成本）。

在S中查找匹配记录的成本将因索引类型而异。如果它是一个B+树，我们将从根开始搜索，并计算需要多少I/O才能到达相应的记录。请参阅B+树课程笔记中的群集和计数I/O部分。

6 哈希连接 SHJ GHJ

请注意，在整个序列中，我们确实在寻找匹配的记录。不过，哈希表非常适合查找匹配项；即使我们没有索引，我们也可以在R的记录上构造一个B-2页2大的哈希表，将其放入内存，然后读入S的每个记录，并在R的哈希表中查找，看看是否可以找到任何匹配项。这称为朴素哈希连接。其成本为[R]+[S] I/O。

这实际上是我们做过的最好的一次。它高效、廉价、简单。然而，这有一个问题；这依赖于R能够完全适应内存（具体而言，R是≤ B− 2页大）。这通常是不可能的。

为了解决这个问题，我们反复将R和S散列到B-1缓冲区中，这样我们就可以得到≤ B− 2页大，使我们能够将它们放入内存并执行简单的哈希连接。更具体地，考虑每对对应的分区$R_i$和$S_i$（即R的分区i和S的分区i）。如果$R_i$和$S_i$都大于B-2页，则将两个分区散列为较小的分区。否则，如果$R_i$或$S_i$≤ B-2页，停止分区并将较小的分区加载到内存中，以构建内存哈希表，并与该对中的较大分区执行朴素哈希连接。

此过程称为Grace哈希连接，其I/O成本为：哈希的成本加上子节上的原始哈希连接的成本。散列的成本可以根据我们需要在多少分区上重复散列多少次而变化。散列分区P的成本包括我们需要读取P中所有页面的I/O，以及我们需要在散列分区P之后写入所有结果分区的I/I。

每个分区对的朴素散列连接部分成本是完成后在两个分区中读取每个页面的成本。

Grace散列很好，但它对密钥偏移非常敏感，所以在使用该算法时要小心。密钥歪斜是当我们尝试散列但许多密钥进入同一个桶时。当许多记录具有相同的密钥时，会发生密钥偏移。例如，如果我们对只包含“yes”作为值的列进行散列，那么我们可以继续散列，但无论使用哪个散列函数，它们都会在同一个桶中结束。

每个分区对的朴素散列连接部分成本是完成后在两个分区中读取每个页面的成本。

7 排序合并联接 SMJ

有时，我们可以先对R和S进行排序，特别是当我们希望我们的联接表按特定列排序时。在这些情况下，我们首先对R和S进行排序，然后：

我们从R和S的开始处开始，前进一个或另一个，直到我们完成一次匹配（如果$r_i$＜$s_j$，则前进R；否则如果$r_i$＞$s_j$，前进S–我们的想法是前进两个中较小的一个，直至我们完成一次匹配）。
现在，让我们假设我们得到了一个匹配。假设这对是$r_i$，$s_j$。我们将S中的这一点标记为标记（s），并检查s中的每个后续记录（$s_j$，$s_j$+1，$s_j$+2等），直到找到不匹配的记录（即读取S中与$r_i$匹配的所有记录）。
现在，转到R中的下一个记录，返回到S中的标记点，并在步骤1再次开始（除了不是从R的开始和S的开始，而是在我们刚刚指出的索引处开始），其思想是，因为R和S被排序，所以R的任何未来记录的任何匹配都不能在S中的标定点之前，因为该记录$r_i$+1≥ $r_i$–如果$r_i$的匹配项在标记之前不存在，则$r_i$+1的匹配项也不可能在标记之前存在！因此，我们从S中的标记点开始滚动，直到找到$r_i$+1的匹配项。

这称为排序合并连接，平均I/O成本为：排序R的成本+排序S+（[R]+[S]）（但需要注意的是，这不是最坏的情况！）。在最坏的情况下，如果R的每个记录都与S的每个记录匹配，则最后一项变成|R|∗ [S] 。最坏情况下的成本是：排序R的成本+排序S+的成本（[R]+|R|）∗ [S] ）。但这通常不会发生）。

让我们看一个例子。让左边的表是R，右边的表是S。

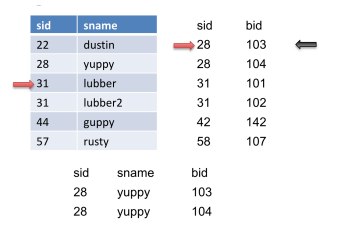
我们将在S上前进指针（红色箭头），因为28＜31，直到S到达31的sid。然后我们将标记此记录（黑色箭头）。此外，我们将输出此匹配。

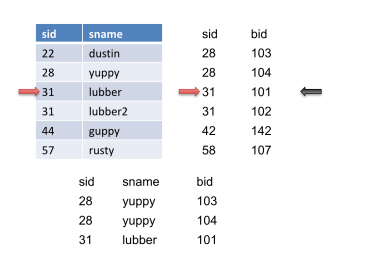
然后我们将再次将指针前进到S上，并获得另一个匹配并输出它。

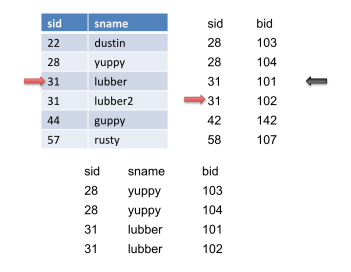
我们再次将指针前进到S上，但没有得到匹配。然后我们将S重置到标记的位置（黑色箭头），然后前进R。当我们前进R时，我们得到另一个匹配，因此我们输出它。

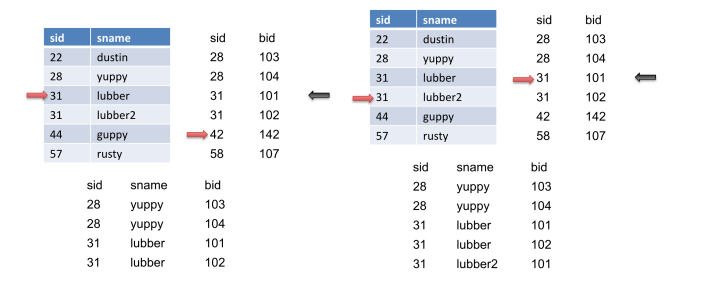
然后我们前进S，得到另一个匹配，然后输出它。

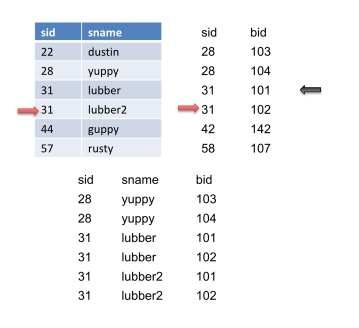
7.1重要的改进

一个重要的改进：您可以将最后一个排序阶段与合并阶段结合起来，前提是您有足够的内存空间为每次运行[R]和每次运行[S]分配一个页面。最后的合并过程是为每次运行R和每次运行S分配一个页面。在此过程中，您节省2∗ （[R]+[S]）I/O

要执行优化，我们必须 :

对[R]和[S]进行排序（分别使用它们的完整缓冲池），直到它们都“几乎已排序”；也就是说，对于｛R，S｝中的每个表T，继续合并T的运行，直到到达倒数第二步，其中再进行一次排序将导致排序表T。
查看剩余[R]的运行次数和[S]的运行数量；把他们加起来。为每次运行分配一页内存。如果您有足够的输入缓冲区来容纳它（即，如果运行（R）+运行（S））≤ B− 1），则可以使用优化，然后可以节约2∗ （[R]+[S]）I/O。
如果您无法进行上一步中描述的优化，则意味着runs（R）+runs（S）≥ B、在理想情况下，优化允许我们避免对R和S进行额外的读取，但这在这里是不可能的，因为我们没有针对R和S的每次运行的可用缓冲区。

然而，我们还没有选择！如果我们不能避免R和S的额外读取，也许我们可以避免其中至少一个的额外读取。因为我们试图最小化I/O，我们希望避免对较大的表R进行额外的读取。它是否可以帮助我们对较小的表S进行完全排序，并将其用于优化？

事实证明我们可以！如果我们对S进行完全排序，根据定义，现在该表只有一次排序运行，这意味着我们只需要在缓冲区中为它分配一个页面。因此，如果运行（R）+1≤ B− 1，然后我们可以为S和R的每次运行分配一个缓冲页。然后，我们可以执行SMJ优化。在这里，我们通过将R与连接阶段相结合，避免了R的最终排序过程。所以我们节省了2∗[R] 页面。

但是，有时，即使这样也不够——如果运行（R）=B-1，那么我们没有用于S的备用缓冲页。在这种情况下，我们仍然希望尽可能减少I/O，因此可能执行上一段中描述的过程，但对于较小的表。即，如果运行（S）+1≤ B− 1，然后对R进行排序，根据定义将其排序运行的数量减少到1，然后为R分配一个缓冲页，为S的每次运行分配一个。然后，执行优化–这将使我们能够通过将其与连接阶段相结合来避免S的最终排序过程，从而节省2∗ [S] I/O。

但是，如果这些条件都不满足，我们将无法优化排序合并联接。没关系。有时候，我们不得不忍着风险，接受我们不能总是走捷径。

wys的个人博客

数据库————迭代器和连接