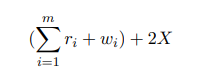哈希
1 动机
有时,排序对于这个问题来说有点过分。在许多情况下,我们只想将相同的值分组在一起,但实际上并不关心值的出现顺序(考虑分组方式或重复数据消除)。在数据库中,将类似的值分组在一起称为哈希。我们无法以您在61B中学习的标准方式构建哈希表,原因与我们无法在最后一个注释中使用快速排序相同;我们无法将所有数据存储在内存中!让我们看看如何构建一个高效的基于外存的散列算法。
2 总体战略
因为我们不能一次将所有数据放入内存,所以我们需要构建几个不同的哈希表并将它们连接在一起。但这个想法有一个问题。如果我们构建两个单独的哈希表,每个哈希表中都有相同的值(例如,“Brian”出现在两个表中),会发生什么?连接这些表将导致一些“Brian”不在彼此旁边。
为了解决这个问题,在用内存中的数据构建哈希表之前,我们需要保证,如果某个值在内存中,那么它的所有出现都在内存中。换句话说,如果“Brian”至少在内存中出现一次,那么我们只能在数据中每次出现“Brian”,当前都在内存中的情况下构建哈希表。这确保了值只能出现在一个哈希表中,从而使哈希表可以安全连接。
3 算法
我们将使用分而治之的算法来解决这个问题。“划分”阶段将划分传递,“控制”阶段将实际构建哈希表。就像在排序注释中一样,我们假设我们有B个缓冲帧可用
第一次分区传递将每个记录散列到B− 1个分区。分区是一组页面,使得页面上的值都散列为相同的值(对于用于构造分区的散列函数)。我们通过使用B− 1输出缓冲器来实现这一点。当输出缓冲区填满时,我们将页面刷新到磁盘。当下一次缓冲区填满时,我们将其放置在之前从同一缓冲区刷新到磁盘的页面旁边。每个分区最重要的属性是,如果某个值出现在该分区中,那么数据中该值的所有出现都会出现在该区域中。换句话说,如果“Brian”出现在该分区中,“Brian”将不会出现在任何其他分区中。这是因为“Brian”总是散列到相同的值,因此它不可能在不同的分区中结束。我们只有B− 1分区,因为我们需要保存一个缓冲帧作为输入缓冲区。
在第一次分区之后,我们可以直接进入哈希表构建阶段,为适合内存的分区构建哈希表。内存匹配是什么意思?内存匹配意味着分区必须小于等于B页。对于太大的分区,我们只需使用与第一次使用的哈希函数不同的哈希函数来重新分区。为什么要使用不同的哈希功能?如果我们重用原始函数,每个值都会散列到其原始分区,因此分区不会变小。我们可以根据需要进行多次递归分区,直到所有分区最多有B个页面。
现在我们所有的分区都可以放在内存中,我们知道所有类似的值都出现在同一个分区中。剩下要做的就是为每个分区构建一个哈希表,并将每个哈希表写入磁盘。
4 例子
在下面的示例中,我们将假设我们有B=3个可用的缓冲页。我们还假设Brian和Eric对第一个哈希函数的值相同,但对第二个哈希函数使用不同的值,Jamie和Lakshya对第一个hash函数使用相同的值。
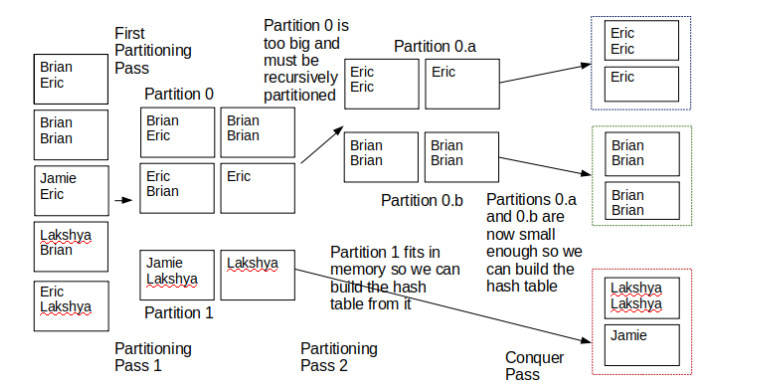
您可以看到分区0太大,因为它包含4个页面,但我们只有3个缓冲帧可用。然而,当它被递归分区时,子分区(0.a和0.b)都只有2页长,因此它们现在可以放入内存。您还可以看到,在最后一次“控制”之后,所有类似的值都彼此相邻,这是我们的最终目标。
5 外部哈希分析
我们不能像排序算法那样创建一个简单的公式来计算I/O的数量,因为我们不知道分区有多大。我们首先需要认识到的一点是,在分区通过后,表中的页面数可能会增加。要了解原因,请考虑下表,其中我们可以在一个页面上拟合两个整数:
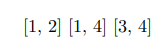
假设B=3,因此我们只将数据划分为2个分区。假设1和3哈希到分区1,2和4哈希到分区2。分区后,分区1将具有:
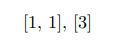
分区2将有:
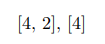
请注意,我们现在只有4个页面,而我们刚开始时只有3个页面。因此,计算I/O数量的唯一可靠方法是遍历每一轮,查看将读取和写入的内容。设m为所需的分区轮数,设$r_i$为分区轮数 $i$ 需要读入的页面数,设$w_i$为需要从分区轮数 $i$ 中写入的页面数;设X为分区后需要构建哈希表的页面总数。以下是I/O数量的公式: