排序
在CS61B中,您了解了许多不同的排序算法。为什么我们在这节课上又学了一个新的?所有传统的排序算法(即快速排序、插入排序等)都依赖于我们能够将所有数据存储在内存中。这是我们在开发数据库时没有的奢侈。事实上,在大多数情况下,我们的数据将比我们可用的内存大一个数量级。
1 I/O Review
请记住,无论何时从内存向磁盘写入页面或从磁盘向内存读取页面,都会产生1个I/O。由于进入磁盘非常耗时,在分析算法性能时,我们只考虑算法产生的I/O数量,而不是像big-O这样的传统算法复杂性度量。因此,在开发我们的排序算法时,我们将尝试最小化它将导致的I/O数量。在计算I/O时,我们忽略缓冲区管理器进行的任何潜在缓存。这意味着,一旦我们解开页面并说我们已经使用它,下一次尝试访问页面时,它将总是花费1个I/O。
2.双向外部合并排序
让我们从开发一个排序算法开始,该算法可以工作,但不尽可能好。因为我们不能一次将所有数据保存在内存中,所以我们知道我们将分别对数据的不同部分进行排序,然后将它们合并在一起。
为了有效地合并两个列表,必须首先对它们进行排序。这意味着排序算法的第一步应该是对每个页面上的记录进行排序。我们将第一阶段称为“控制”阶段,因为我们正在控制单个页面。
之后,让我们开始使用合并排序中的合并算法将页面合并在一起。我们将调用这些合并排序运行的结果。排序运行是一系列已排序的页面。
算法的其余部分将只是继续合并这些排序运行,直到只剩下一个排序运行。一次排序运行意味着我们的数据已完全排序!请参阅下一页的图像,了解算法运行到完成的图表。
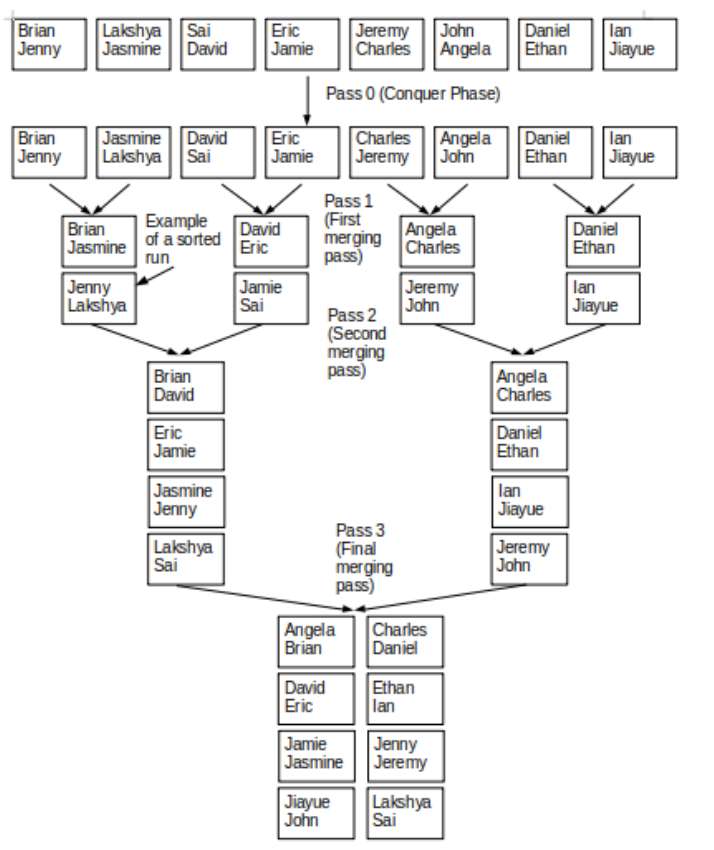
3.双向合并分析
在分析数据库算法时,最重要的度量是该算法使用的I/O数量,因此让我们从这里开始。首先,请注意,每次传递数据都需要2∗ N个I/O,其中N是数据页的数量。这是因为对于每一次传递,我们需要读入每一页,并在修改后写回每一页。
剩下要做的唯一一件事就是计算出我们需要多少次传递才能对表进行排序。我们总是需要做最初的“控制”,所以我们总是至少有一个传递。现在,需要多少次合并过程?每通过一次,我们将剩下的排序运行数量减半。每次对数据进行分割都会向您显示日志,因为我们将其除以2,所以日志的基数将为2。接着我们需要$\lceil log_2(N) \rceil $次传递,总共$\lceil 1+log_2(N) \rceil $次传递。所以我们总共需要 $2N*(1+\lceil log_2(N) \rceil)$ 次I/O(注意:传递0,即初始控制通过,在外部排序中计算为一次传递,并作为I/O成本公式中的一个传递)。
现在,让我们分析执行该算法需要多少缓冲页。请记住,缓冲页或缓冲帧是内存中页的slot 。
第一次传递,即“控制传递”,对每个页面进行单独排序。这意味着我们只需要一个缓冲页来保存我们正在排序的页面!
现在让我们分析合并过程。回想一下合并排序中合并的工作方式。我们只比较合并的两个列表中的第一个值。这意味着我们只需要在内存中存储每个排序运行的第一页,而不是整个排序运行。当我们浏览了一个页面中的所有记录后,我们只需从内存中删除该页面,并加载到排序运行的下一个页面。到目前为止,我们需要2个缓冲页(每个排序运行1个缓冲页)。我们将调用缓冲帧,用于存储每个排序运行的输入缓冲区的前端。
我们现在唯一缺少的是一个存储输出的地方。我们需要在某个地方写入记录,因此我们需要另外一个页面,称为输出缓冲区。每当这个页面填满时,我们就将它刷新到磁盘并开始构建下一个页面。总的来说,我们有两个输入缓冲区和一个输出缓冲区,每个合并过程总共需要3个页面。我们通常有超过3个页面可用于内存排序,因此该算法没有利用我们所有的内存。让我们构造一个更好的算法,使用我们所有的内存。
4完全外部排序
假设我们有B个缓冲区页面可用。我们将进行的第一个优化是在初始的“控制过程”中。我们不只是对单个页面进行排序,而是加载B页面并将它们一次排序到一个排序运行中。这样,我们将在第一次通过后产生更少和更长的排序运行。
第二个优化是一次合并两个以上的排序运行。我们有B个可用的缓冲帧,但输出缓冲区需要1。这意味着我们可以有B-1输入缓冲区,因此可以一次合并B-1排序运行。假设我们有4个可用的缓冲帧,请参阅下一页的此类图表。
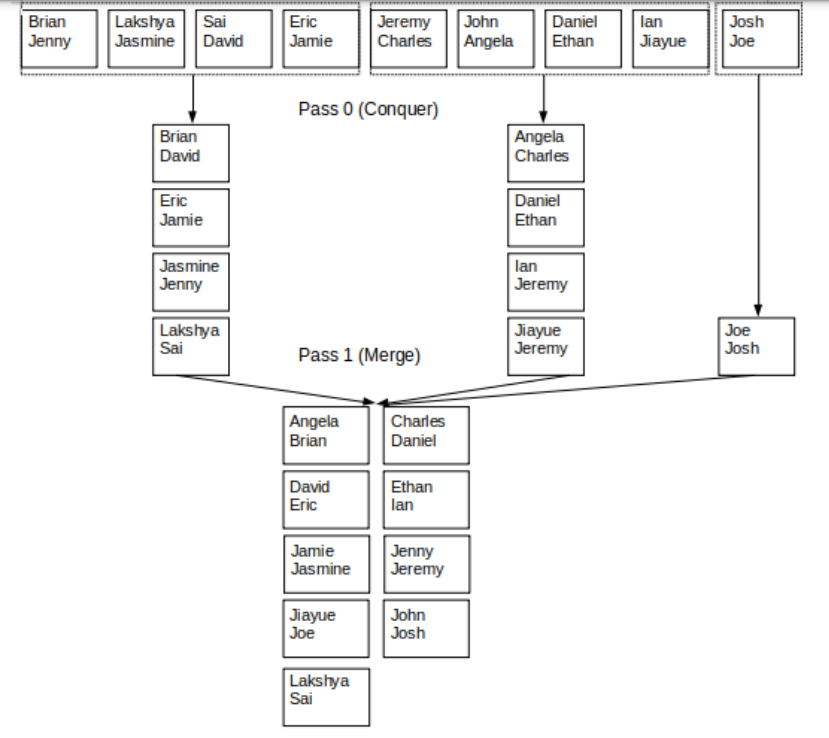
现在,我们在控制阶段一次取4页,并输出长度为4的排序运行。在合并过程中,我们可以一次合并征服过程中产生的所有三个排序块。这将通过次数(因此我们的I/O)减少了一半!
5.完全外部合并排序的分析
现在,让我们计算一下改进后的排序使用与双向合并相同的进程需要多少I/O。控制传递现在只生成$\lceil N/B \rceil$排序的运行,因此我们要合并的运行较少。在合并过程中,我们将排序的运行数除以B−1而不是2,因此日志的基础需要更改为B− 1.这使得我们的整体排序采用$1+\lceil log_{B−1}\lceil N/B\rceil$ 传递,因此总共$2N*(1+\lceil log_{B−1}\lceil N/B\rceil)$次I/O。