B+ 树
1 简介
在前面的笔记中,我们讨论了数据存储的不同文件和记录表示。本周,我们将介绍索引,它是一种在数据文件之上运行的数据结构,有助于加快对特定键的读取。您可以将数据文件视为书籍的实际内容,将索引视为快速查找的内容表。我们使用索引使查询运行得更快,尤其是那些频繁运行的查询。考虑一个web应用程序,它在登录过程中根据用户名在用户表中查找用户的记录。用户名列上的索引将通过快速查找试图登录的用户的行来加快登录速度。在本课程注释中,我们将学习B+树,这是一种特定类型的索引。下面是一个B+树的示例:
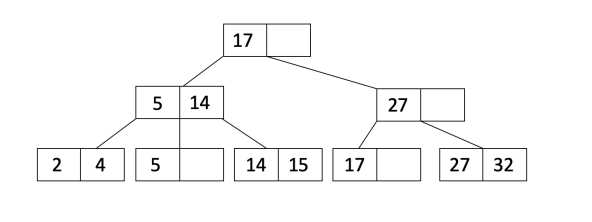
2 属性
- d是B+树的阶,每个节点(根节点除外)必须有 $d \leq x \leq 2d$ 项,如果没有删除发生的话(删除数据后叶子节点可能少于d项)。节点中的项必须排序。
- 在内节点的两项之间有一个指针指向孩子节点,因为最多有2d项在节点中,内节点最多有2d+1个指针指向孩子节点。这也被称为树的扇出。
- 条目左侧子结点中的键必须小于条目,而右侧子节点中键必须大于或等于条目。
- •所有叶片深度相同,且具有d和2d个条目(即至少半满)
举个例子,一个阶为2的树:
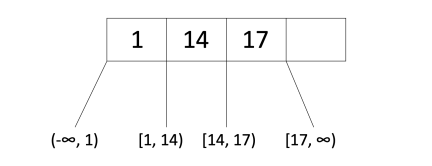
请注意,节点满足阶要求(d≤ x≤ 2d),因为d=2并且该节点具有3个条目满足2≤ x≤ 4.
- 由于sorted和children属性,我们可以遍历树到叶子,以找到所需的记录。这类似于BST(二进制搜索树)。
- 每个根到叶路径都有相同数量的边-这是树的高度。从这个意义上说,B+树总是平衡的。换句话说,只有根节点的B+树的高度为0。
- 只有叶节点包含记录(或指向记录的指针-这将在后面解释)。内部节点(即非叶节点)不包含实际记录。
3 插入
要在B+树中插入条目,请执行以下步骤:
(1) 找到要插入值的叶节点L。您可以通过遍历树来实现这一点。按顺序将键和记录添加到叶节点。
(2) 如果L溢出(L超过2d项)
(a)分成$L_1$,$L_2$。 $L_1$中保持d个条目,这意味$L_2$中为d+1。
(b) 如果L是叶节点,则将$L_2$的第一个条目复制到父节点中。如果L不是叶节点,则将$L_2$的第一个条目移动到父节点中。
(c) 调整指针。
(3) 如果父节点溢出,则通过对父节点执行步骤2来递归。(这是增加树高的唯一情况。)
注意:我们希望将叶节点数据复制到父节点中,以便不丢失叶节点中的数据。请记住,建立索引的表中的每个键都必须位于叶节点中!处于内部节点并不意味着键实际上仍在表中。另一方面,我们可以将内部节点数据移动到父节点中,因为内部节点不包含实际数据,它们只是遍历树时搜索方法的参考。
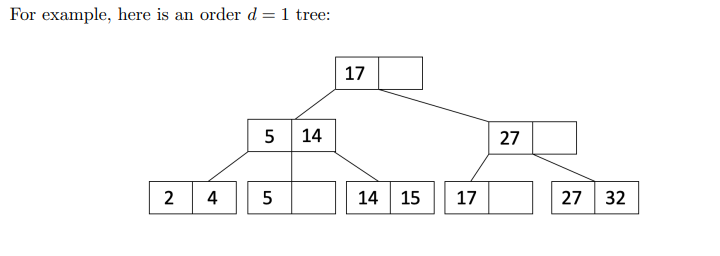
让我们看一个例子来更好地理解这个过程!我们从以下顺序d=1树开始:
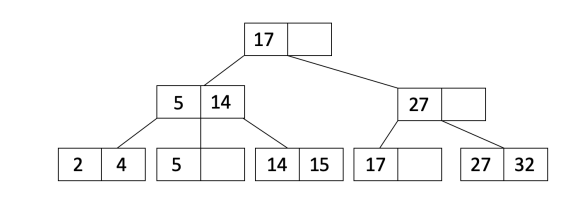
插入19。当插入19,我们可以看到17旁边有个空位。
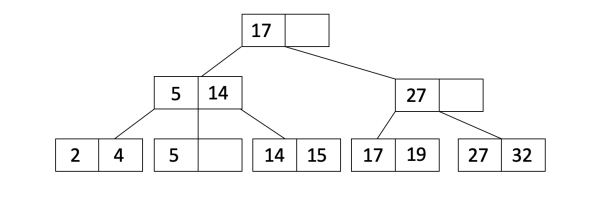
接着我们插入21。当我们插入21, 这会造成叶子节点溢出。而且,我们把叶子节点拆成如下所示:
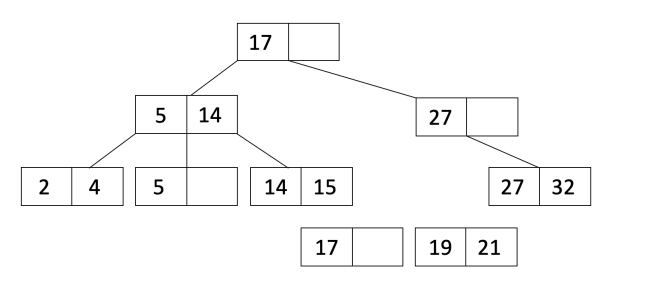
因为我们拆分了叶子节点我们把 $L_2$ 的第一个节点复制到父节点,然后调整指针,然后对父节点排序得到:
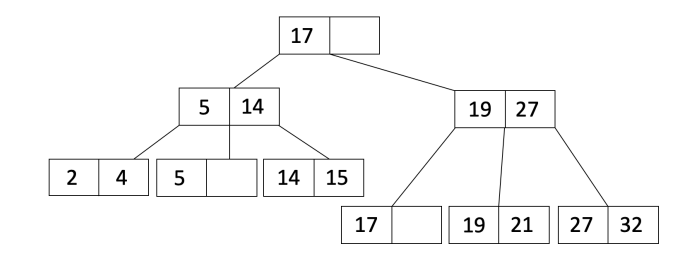
让我们再做一次插入。这次我们将插入36。当我们插入36时,叶溢出,因此我们将执行与插入21时相同的过程以获得:
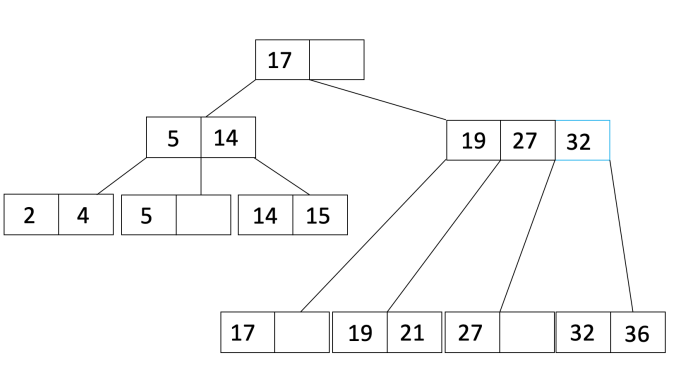
注意,现在父节点溢出,所以现在必须递归。我们将拆分父节点以获得:
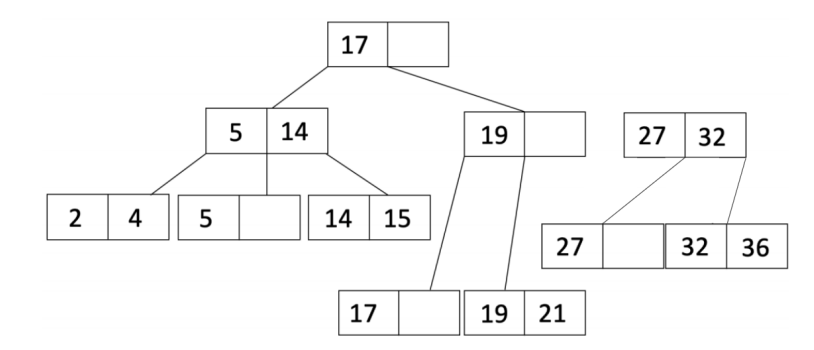
由于是一个内部节点溢出,我们将L2的第一个条目上移到父节点,并调整指针以获得:
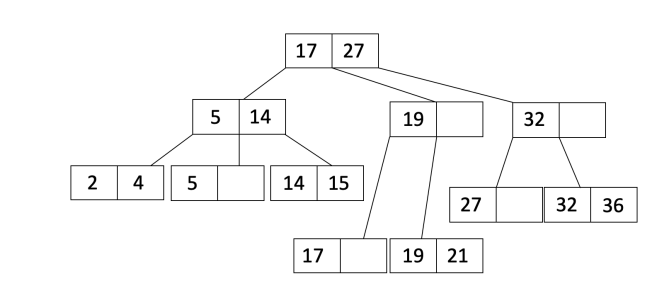
最后,这里有几个关于插入B+树的说明:
通常,B+树节点具有最小的d个条目和最大的2d个条目。在其他换句话说,如果树中的节点在插入之前满足此不变量(通常)则在插入之后,它们将继续满足它。
当节点包含超过2d个条目时,会发生节点插入溢出。
4 删除
要删除一个值,只需找到适当的叶并从该叶中删除不需要的值。这就是它的全部内容。(是的,从技术上讲,我们最终可能会违反B+树的一些不变量。这没关系,因为在实践中,我们得到的插入比删除多得多,所以我们删除的东西会很快被替换。)
提醒:我们从不删除内部节点键,因为它们仅用于搜索,而不用于保存数据。
5 存储记录
到目前为止,我们还没有讨论记录实际上是如何存储在叶子中的。现在让我们来看看。有三种方式将记录存储在叶子中:
- 备选方案1
在备选方案1中,叶页是数据页。叶页不包含指向记录的指针,而是包含记录本身。
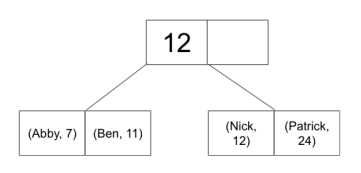
- 备选方案2
在备选方案2中,叶页保存指向相应记录的指针。
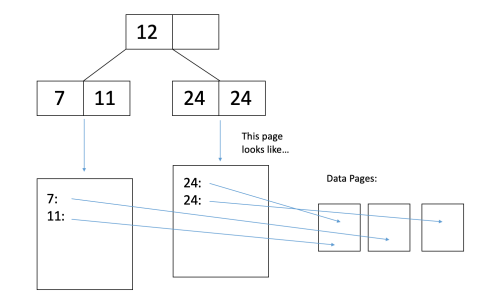
备选方案3
在备选方案3中,叶页保存指向相应记录的指针列表。当有多个记录具有相同的叶节点条目时,这比备选方案2更紧凑。
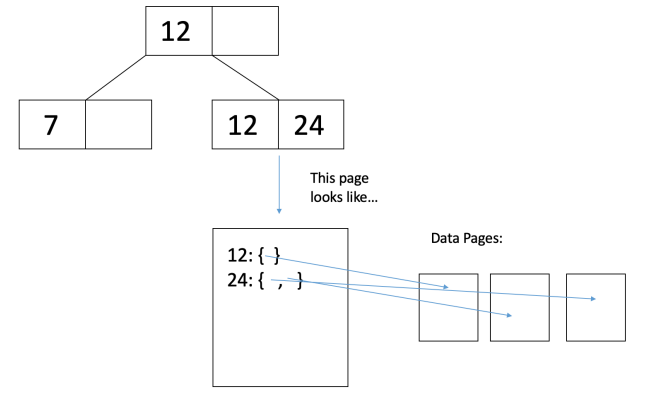
6 聚类
既然我们已经讨论了如何在叶节点中存储记录,我们还将讨论如何组织数据页上的数据。集群/非集群是指数据页的结构。由于叶页是备选1的实际数据页,并且键在索引叶页上排序,因此默认情况下,备选1索引是聚集的。因此,取消群集仅适用于备选方案2或3。
- 未群集
在未群集索引中,数据页完全混乱。因此,很可能您需要为每个记录读取单独的页面。例如,考虑以下示例:
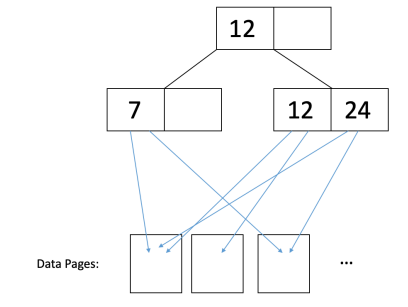
在上图中,如果我们想读取12和24的记录,那么我们必须读取它们指向的每个数据页,以便检索与这些键关联的所有记录。
- 群集
在聚集索引中,数据页在构建B+树的同一索引上排序。这并不意味着数据页被精确排序,只是键的顺序与数据大致相同。因此,I/O成本的差异来自缓存,其中两个具有关闭键的记录可能位于同一页中,因此可以从缓存页读取第二个记录。因此,您通常只需要读取一个页面,就可以获得具有公共/类似密钥的所有记录。例如,考虑以下示例:
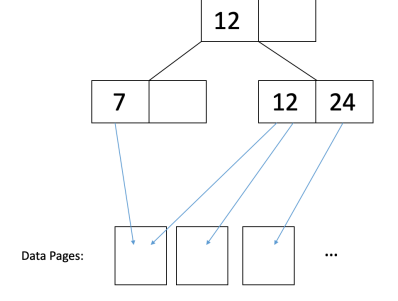
未群集=∼ 每个记录1个I/O。
群集=∼ 每页记录1个I/O。
聚集索引与非聚集索引
虽然聚集索引可以更有效地进行范围搜索,并在顺序磁盘访问和预取等过程中提供潜在的局部性优势,但它们通常比非聚集索引维护成本更高。例如,随着更多插入的到来,数据文件可能变得不那么集群化,因此需要定期对文件进行排序。
7 IO计数
这是一般程序。在备忘单上写下以下内容是一件好事:
(1) 读取相应的根到叶路径。
(2) 读取相应的数据页。如果需要读取多个页面,我们将分配一个读取IO
对于每个页面。此外,我们考虑了备选方案2或3的聚类(见下文)
(3) 如果要修改,请写入数据页。同样,如果我们要进行跨越多个
对于数据页,我们需要为每个页分配一个写IO。
(4) 更新索引页。
让我们看一个例子。参见以下备选方案2未群集的B+树:
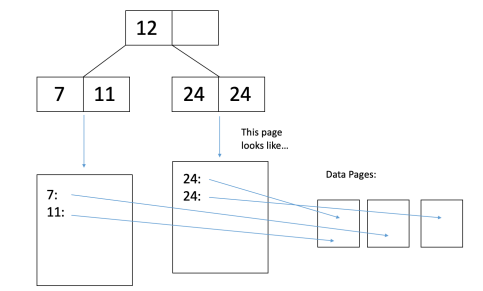
我们想从数据库中删除只有11岁的孩子。需要多少I/O?
2个相关索引页(索引页是内部节点或叶节点)的每一个都有一个I/O。
一个I/O,用于读取11岁儿童记录所在的数据页。一旦记录在内存中,我们可以从页面中删除记录。
一个I/O,将修改后的数据页写回磁盘。
既然我们的数据库中不再有11岁的孩子,我们应该从B+树的叶页中删除键“11”,我们已经在步骤1中读取了该键。我们这样做,然后需要一个I/O将修改后的叶页写入磁盘。
因此,删除记录的总成本为5 I/O。
8 散货装载
我们之前讨论的插入过程对于对现有B+树进行添加非常有用。但是,如果我们想从头开始构建B+树,我们可以做得更好。这是因为如果我们使用插入过程,每次我们想要插入新的东西时,我们都必须遍历树;定期插入随机数据页也会导致缓存效率低下和叶页利用率低下,因为它们通常是半空的。相反,我们将使用批量装载:
(1) 按索引将基于的键对数据进行排序。
(2) 填充叶页直到某个填充因子f。请注意,填充因子仅适用于叶节点。对于内部节点,我们仍然遵循相同的规则进行插入,直到它们满为止。
(3) 添加从父页面到叶页面的指针。如果父级溢出,我们将遵循类似于插入的过程。我们将父节点拆分为两个节点:
(a) 在L1中保留d个条目(这意味着d+1个条目将进入L2)。
(b) 由于父节点溢出,我们将L2的第一个条目移动到父节点中。
(4) 调整指针。
让我们看一个例子。假设我们的填充因子是3/4,我们想将1,…,20插入到一个d=2阶树中。我们将从填充页开始,直到填充因子:
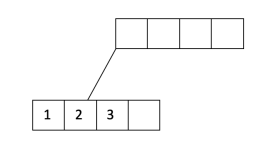
我们已将叶节点填充到填充因子3/4,并添加了从父节点到叶节点的指针。让我们继续填写:
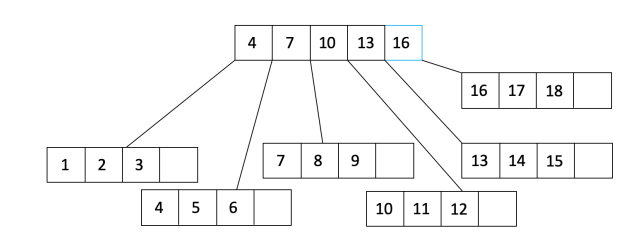
在上图中,我们看到父节点已溢出。我们将父节点拆分为两个节点,并创建一个新的父节点:
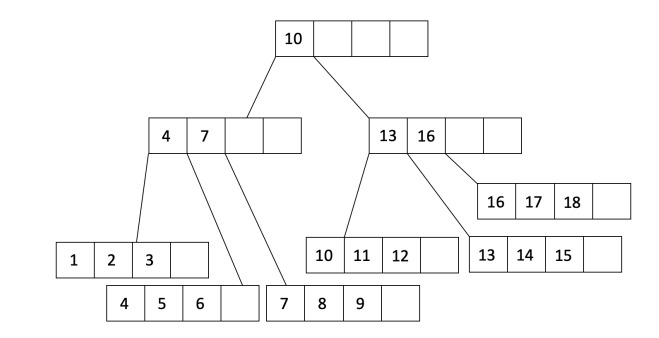
从上面的示例中可以看出,从批量加载构建的索引总是以集群开始,因为基础数据是按键排序的。为了保持聚类,我们可以根据未来的插入模式选择填充因子