wys的个人博客

你有很多事放不下？做人要潇洒一点~

0%

In-Circle

Posted on Edited on In

uva 11524

题意

如图所示， $\triangle{ABC}$ 的内切圆把他的三边分别划分成 $m1:n1$ , $m2:n2$ ,$m3:n3$ 的比例。另外已知内切圆的半径 $r$ ,求 $\triangle{ABC}$ 的面积 。

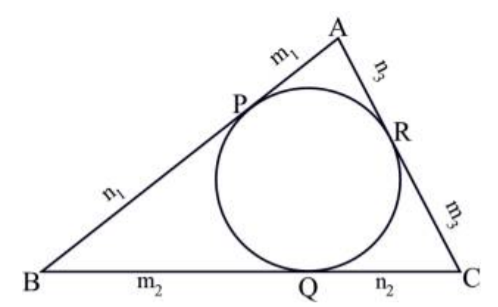
普遍思路

设三角形三边长为 $a$ , $b$ , $c$ 。

由内切圆得三角形的面积为 $S = \frac{(a+b+c)*r}{2}$ 。

由海伦公式得三角形得面积为 $S = \sqrt{p(p-a)(p-b)*(p-c)}$ 。

其中 $p = \frac{a+b+c}{2}$ 。

设 $AP$ 为$m_1x$联立两个方程可以解出 $x$ 从而可以求出答案。

个人思路

个人认为上述方程比较难解，下面给出另一种解法。

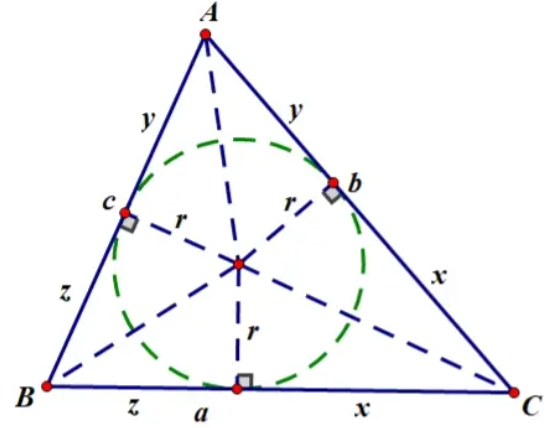
在三角形中有如下结论

$\tan{\frac{A}{2}}\tan{\frac{B}{2}}+\tan{\frac{A}{2}}\tan{\frac{C}{2}}+\tan{\frac{B}{2}}*\tan{\frac{C}{2}} = 1$

$\therefore \frac{1}{\tan{\frac{A}{2}}} + \frac{1}{\tan{\frac{B}{2}}} + \frac{1}{\tan{\frac{C}{2}}} = \frac{1}{\tan{\frac{A}{2}}\tan{\frac{B}{2}}\tan{\frac{C}{2}}}$

而 $\tan{\frac{A}{2}} = \frac{r}{y}$ , $\tan{\frac{B}{2}} = \frac{r}{z}$, $\tan{\frac{C}{2}} = \frac{r}{x}$

代入上式得 $\frac{x+y+z}{r} = \frac{xyz}{r^3}$

即可解出答案。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
#define FOR(i,f_start,f_end) for(int i=f_start;i<=f_end;++i)
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int>PII;
const double eps = 1e-8;
const int maxn = 200000 + 5;
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
//unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
//mt19937 rand_num(seed);



int main(){
    
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);

    //std::ios::sync_with_stdio(false);
    int t;
    cin >> t;
    while(t--){
        double r;
        cin >> r;
        double m1,n1,m2,n2,m3,n3;
        cin >> m1 >> n1 >> m2 >> n2 >> m3 >> n3;
        double p,q;
        p = m2*m2*m1*n2/n1/r/r;
        q = (n1*m2+m1*m2+n1*n2)/n1;
        double x = sqrt(q/p);
        double l = (2*m2 + 2*n2 + m1*m2/n1 + n2*n3/m3)*x/2;
        printf("%.4lf\n",l*r);
    }
    return 0;
}